Les incontournables du TVI
Exercice Bac 2015 : Théorèmes des Valeurs Intermédiaires
Exercice 1
f(x) = x3 + x – 7
1. Montrer que l’équation f(x) = 0 admet une unique solution α sur l’intervalle [ 0 ; 2 ].
2. Proposer un encadrement de α à 10-3 près.
3. En déduire le tableau de signe de f.
4. Montrer que α3 = 7 – α
Exercice 2
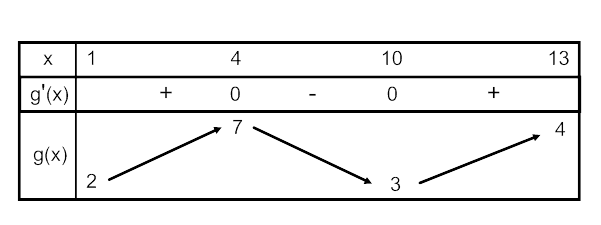
Le tableau de variation de g étant donné,
déterminer le nombre de solutions de l’équation g(x) = 5 .