Quiz sur le théorème des valeurs intermédiaires

Ce quiz est avant tout pour les Terminales. Mais si tues encore en première, tente le! Prendre de l’avance n’est jamais une mauvaise chose…
Avec ce quiz tu réviseras le théorème des valeurs intermédiaire, la continuité ou la discontinuité des fonctions.
Si ce sujet ne te parle pas ou si tu as des difficultés, regarde la vidéo ci-joint avant de commencer. Sinon tu peux aussi aller faire un tour sur notre site leprofduweb.com, il y a 21 autres vidéos pour t’aider à comprendre les fonctions.

Continuité et théorème des valeurs intermédiaires

Départ

Tu t'es frotté au quiz : Continuité et théorème des valeurs intermédiaires.Tu as obtenu %%SCORE%% sur %%TOTAL%%.Je dirais que ta performance est %%RATING%%.

Vos réponses sont surlignées ci-dessous.

Question 1

Qu'entend-on par fonction continue ?

A	La courbe de cette fonction peut être tracée sans jamais lever le crayon
B	Il s'agit d'une fonction linéaire
C	Cette fonction n'a pas de limite

Explication pour la question 1: 

La courbe de cette fonction ne présente aucun "saut". Elle peut être tracée sans jamais lever le stylo.

Question 2

Ces fonctions sont-elles toutes continues sur R ?\begin{equation} \ exp^{x}, \ln(x), \ x^{2} + x^{3} + 7 \end{equation}

A	Non, aucune
B	Certaines oui, d'autres non
C	Oui, toutes

Explication pour la question 2: 

Elles sont toutes continues sur R. Le plus simple est de se demander : "pour quelle valeur, la fonction n'est pas définie ?".

Question 3

\begin{equation} \left(\frac{10x^{4} + 3}{3x^{2}-5}\right) \end{equation}
Cette fonction est-elle continue sur R ? Ou sur d'autres intervalles ? (2 réponses exactes)

A	Elle est continue sur R
B	Il n'existe aucun intervalle où cette fonction est continue
C	Non elle n'est pas continue sur R
D	Cette fonction est continue sur 2 intervalles: \begin{equation} \ ] -\infty ; \sqrt { \left(\frac{5}{3}\right)} [ \quad U \quad ] \sqrt { \left(\frac{5}{3}\right)} ; +\infty [ \end{equation}

Explication pour la question 3: 

Cette fonction n'est pas définie sur R à cause de son dénominateur égal à 0 lorsque : \begin{equation} \ x = \sqrt { \left(\frac{5}{3}\right)} \end{equation}
Cependant, elle est continue sur les 2 intervalles qui ne prennent pas en compte cette valeur.

Question 4

Si une droite est continue sur R et qu'elle passe par les valeurs 100 et 700, passera t-elle par 300, 400 et 900?

A	Elle passera forcément par les valeurs 300 et 400 mais ne passera dans aucun cas par 900.
B	Elle passera forcément par les valeurs 300 et 400 et elle pourrait passer par la valeur 900
C	Elle peut ne pas passer par ces 3 valeurs.
D	Elle passera forcément par ces 3 valeurs

Explication pour la question 4: 

Elle passera par 300 et 400, c'est obligatoire. Par contre, rien n’empêche qu'elle passe aussi par 900. Elle aurait été strictement croissante sur R, cela aurait été impossible mais là, elle peut d'abord être croissante jusqu'à 900 et devenir décroissante pour atteindre 700.

Question 5

La question précédente s'appuyait sur le théorème des valeurs intermédiaires. Donne moi sa définition. (2 réponses possibles)

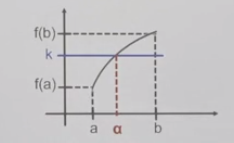
A	f est une fonction. Si f est continue et strictement croissante sur [ a ; b ] et f(a) < k < f(b) alors : il existe une et une seule solution alpha à l'équation f(x) = k.
B	f est une fonction. Si f est continue et strictement décroissante sur [ a ; b ] et f(b) < k < f(a) alors : il existe une et une seule solution alpha à l'équation f(x) = k.
C	f est une fonction. Si f est continue et croissante sur [ a ; b ] et f(a) < k < f(b) alors : il existe une et une seule solution alpha à l'équation f(x) = k.
D	f est une fonction. Si f est continue et décroissante sur [ a ; b ] et f(a) < k < f(b) alors : il existe une et une seule solution alpha à l'équation f(x) = k.

Explication pour la question 5: 

Ces deux définitions sont à connaître par cœur !!! Si l'on retire le "strictement" la courbe f peut avoir une pente égale à 0. 2 valeurs peuvent donc avoir la même image. k peut donc avoir plusieurs solutions.

Question 6

Quels sont les intérêts du théorème des valeurs intermédiaires?

A	Pour la résolution de l'équation : on sait que la solution existe et que la solution est unique (unicité)
B	Pour la résolution de l'équation : on sait qu'il y a une ou plusieurs solutions
C	Pour la résolution de l'équation : on sait qu'il y a une solution au maximum mais il peut aussi, ne pas en avoir

Explication pour la question 6: 

On l'a vu dans la question précédente, k n'a qu'une et une seule solution et elle existe forcément.

Question 7

Prenons cette équation : \begin{equation} \ \frac{x^{3}}{2} + 2x + 8 \end{equation}
On sait que f(5) = 80.5 et f(0) = 8
Que peut-on dire, sans le calculer, de \begin{equation} \ f(\pi) \end{equation}

A	on ne peut pas savoir
B	Sa valeur se situe entre 0 et 80.5
C	Sa valeur est supérieure à 80.5
D	Sa valeur est inférieure à 0

Explication pour la question 7: 

D'après le théorème des valeurs intermédiaires, sa valeur est bien située entre 0 et 80.5 car la fonction est strictement croissante et continue sur R
ET 0 < pi < 5.

Une fois terminé, cliquez sur le bouton ci-dessous. Toutes les questions que vous n'avez pas complétées sont marquées comme incorrectes. Obtenir les résultats

Il y a 7 questions à compléter.

←

→

Vous avez complété

questions

question

Votre score est de

Correct

Faux

Réponse partielle

Vous n'avez pas fini votre quiz. Si vous quittez cette page, votre progression sera perdue.

Réponses correctes

Vous avez sélectionné

Pas essayer

Score final du quiz

Nombre de questions répondues de manière correcte

Nombre de questions répondues de manière incorrecte

Question non répondues

Nombre total de questions dans le quiz

Détail de la question

Résultats

Date

Score

Indice

Temps autorisé

minutes

secondes

Temps utilisé

Réponse(s) sélectionnée(s)

Texte de la question

Fini

améliorable, il faut revoir tes cours

pas mal : il faut persévérer

moyenne !

bonne !

parfaite !